Занимательная физика. Книга 1 - Страница 5

То, что это действительно так, легко понять на простом опыте, который следует проделать при удобном случае. Воткните в землю палку рядом с колесом стоящей телеги так, чтобы палка приходилась против оси. На ободе колеса, в самой верхней и в самой нижней его частях, сделайте пометки мелом или углем; пометки придутся, следовательно, как раз против палки. Теперь откатите телегу немного вправо (рис. 7), чтобы ось отошла от палки сантиметров на 20–30, и заметьте, как переместились ваши пометки. Окажется, что верхняя пометка A переместилась заметно больше, нежели нижняя В, которая только едва отступила от палки.

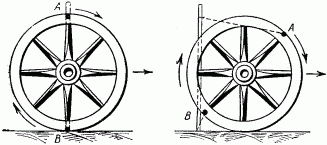
Рис. 7. Как убедиться, что верхняя часть колеса движется быстрее нижней Сравните расстояния точек А и В откатившегося колеса (правый чертеж) от неподвижной палки.

Самая медленная часть колеса

Итак, не все точки движущегося колеса телеги перемещаются одинаково быстро. Какая же часть катящегося колеса движется всего медленнее?

Нетрудно сообразить, что медленнее всех движутся те точки колеса, которые в данный момент соприкасаются с землей. Строго говоря, в момент соприкосновения с почвой эти точки колеса совершенно неподвижны.

Все сказанное справедливо только для колеса катящегося, а не для такого, которое вращается на неподвижной оси. В маховом колесе, например, верхние и нижние точки обода движутся с одинаковой скоростью.

Задача не шутка

Вот еще одна не менее любопытная задача: в поезде, идущем, скажем, из Ленинграда в Москву, существуют ли точки, которые по отношению к полотну дороги движутся обратно — от Москвы к Ленинграду?

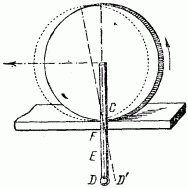
Рис. 8. Опыт с кружком и спичкой. Когда колесо откатывается налево, точки F, Е, D выступающей части спички подвигаются в обратную сторону.

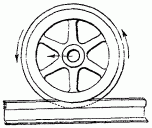
Рис. 9. Когда железнодорожное колесо катится налево, нижние части его выступающего края движутся направо, т. е. в обратную сторону.

Оказывается, что в каждый момент на каждом колесе существуют такие точки. Где же они находятся?

Вы знаете, конечно, что железнодорожные колеса имеют на ободе выступающий край (реборду). И вот оказывается, что нижние точки этого края при движении поезда перемещаются вовсе не вперед, а назад.

В этом легко удостовериться, проделав такой опыт. К небольшому кружочку, например к монете или пуговице, прилепите воском спичку так, чтобы она прилегала к кружку по радиусу и далеко выступала за край. Если теперь упереть кружок (рис. 8) в край линейки в точке С и начать катить его справа налево, то точки F, Е и D выступающей части отодвинутся не вперед, а назад. Чем дальше точка от края кружка, тем заметнее подастся она назад при качении кружка (точка D перейдет в D').

Точки реборды железнодорожного колеса движутся так же, как и выступающая часть спички в нашем опыте.

Вас не должно удивлять теперь, что в поезде существуют точки, которые движутся не вперед, а назад.

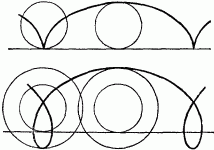
Рис. 10. Вверху изображена та кривая линия («циклоида»), которую описывает каждая точка обода катящегося колеса телеги. Внизу — кривая линия, описываемая каждой точкой выступающего края железнодорожного колеса.

Правда, это движение длится лишь ничтожную долю секунды; но, как бы то ни было, обратное перемещение в движущемся поезде все же существует наперекор нашим обычным представлениям. Сказанное поясняется рисунками 9 и 10.

Откуда плыла лодка?

Вообразите, что весельная лодка плывет по озеру, и пусть стрелка а на нашем рис. 11 изображает направление и скорость ее движения. Наперерез идет парусная лодка; стрелка b изображает ее направление и скорость. Если вас, читатель, спросят, откуда эта лодка отчалила, вы, конечно, сразу укажете пункт м на берегу. Но если с тем же вопросом обратиться к пассажирам весельной лодки, они указали бы совершенно другую точку. Почему?

Рис. 11. Парусная лодка идет наперерез весельной. Стрелки а и b — скорости. Что увидят гребцы?

Происходит это оттого, что пассажиры видят лодку движущейся вовсе не под прямым углом к пути своей лодки. Они ведь не чувствуют собственного движения: им кажется, что сами они стоят на месте, а все кругом движется с их собственной скоростью, но в обратном направлении. Поэтому для них парусная лодка движется не только по направлению стрелки b, но и по направлению пунктирной линии а, обратно движению весельной лодки (см. рис. 12). Оба движения парусной лодки — действительное и кажущееся — складываются по правилу параллелограмма. В результате пассажирам шлюпки кажется, будто парусная лодка движется по диагонали параллелограмма, построенного на b и а. Вот почему пассажирам представляется, что парусная лодка отчалила от берега вовсе не в точке М, а в некоторой точке N, далеко впереди по движению весельной шлюпки (рис. 12).

Двигаясь вместе с Землей по ее орбите и встречая лучи звезд, мы судим о положении источников этих лучей так же неправильно, как пассажиры весельной лодки ошибочно определяют место отплытия парусной. Поэтому звезды представляются нам немного смещенными вперед по пути движения Земли. Конечно, скорость движения Земли ничтожна по сравнению со скоростью света (в 10000 раз меньше); поэтому кажущееся смещение звезд незначительно. Но оно может быть обнаружено с помощью астрономических приборов. Явление это носит название аберрации света.